[프로그래머스] 피로도

1. 문제

프로그래머스

2. 핵심 아이디어

완전탐색 순열 DFS

3. 코드

[순열]

import Foundation

func solution(_ k:Int, _ dungeons:[[Int]]) -> Int {
    let dungeonPermutaion = permutation(dungeons, dungeons.count)
    var maxEnterTimes = 0
    for dungeonList in dungeonPermutaion {
        var userFatigue = k
        var enterTimes = 0
        for dungeon in dungeonList {
            let enterFatigue = dungeon[0]
            let consumeFatigue = dungeon[1]
            if userFatigue >= enterFatigue {
                userFatigue -= consumeFatigue
                enterTimes += 1
            }
        }
        if enterTimes > maxEnterTimes {
            maxEnterTimes = enterTimes
        }
    }
    return maxEnterTimes
}

[DFS]

import Foundation

func solution(_ k:Int, _ dungeons:[[Int]]) -> Int {
    let visited = Array(repeating: false, count: dungeons.count)
    var maxDepth = 0
    func DFS(visited: [Bool], fatigue: Int, depth: Int) {
        if depth > maxDepth {
            maxDepth = depth
        }
        for i in 0..<dungeons.count {
            let enterFatigue = dungeons[i][0]
            let consumeFatigue = dungeons[i][1]
            if !visited[i] && fatigue >= enterFatigue {
                var cVisited = visited
                cVisited[i] = true
                DFS(visited: cVisited, fatigue: fatigue - consumeFatigue, depth: depth + 1)
            }
        }
    }
    DFS(visited: visited, fatigue: k, depth: 0)
    return maxDepth
}

4. 풀이 과정

처음에는 다음과 같이 생각하여 정리하였다.

필요사항:

 최소 필요 피로도: 던전 탐험을 위한 피로도
 소모 피로도: 던전 탐험 후 소모되는 피로도
 유저가 탐험할 수 있는 최대 던전 수

우선 시 되는 것: 소모 피로도가 낮은 것.
- 소모 피로도 1순위, 최소 필요 피로도 2순위로 정렬.
- 선택을 해나가면서 가능한 던전 탐색.

이런식으로 정렬을 사용해서 문제를 풀면 어떨까 생각을 했었는데,

생각해보니 이렇게 풀면 던전을 방문하는 순서를 커버할 수가 없어서, 틀리게 된다.

그래서 순열로 던전에 방문하는 모든 순서를 구해서 탐색하는 것을 생각했고, 해당 코드가 위에 있다.

그런데 이렇게 풀면 모든 경우의 수를 다 탐색을 하는거라 상당히 비효율적 일 것이라 생각했다.

그래서 DFS 로 다시 한번 풀어보고 테스트 했다.

순열	DFS

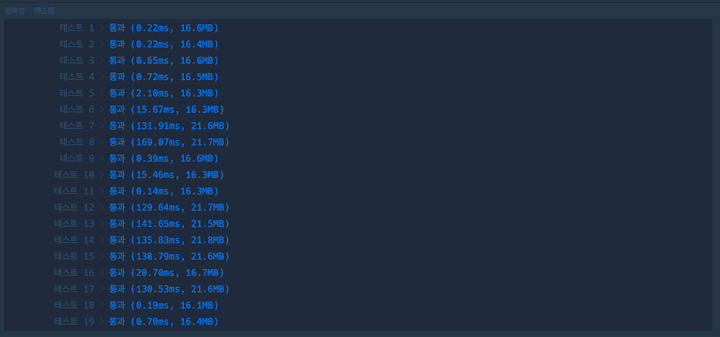
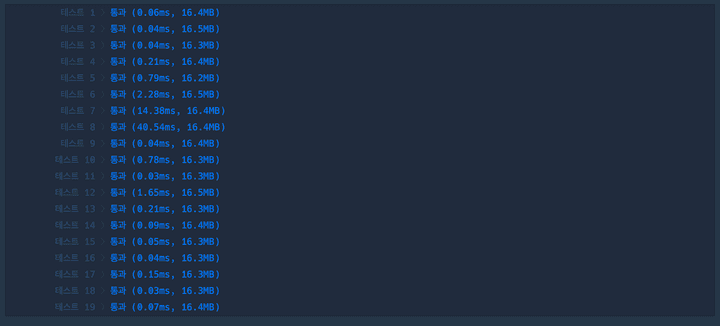
차이가 엄청나다!!

순열은 정말 어쩔 수 없을 때 사용하자..

그리고 또 하나 발견한 것이 enumerated 에 관한 것인데,

애가 엄청난 시간을 잡아먹는다는 것을 이번에 발견했다.

DFS Enumerated	DFS

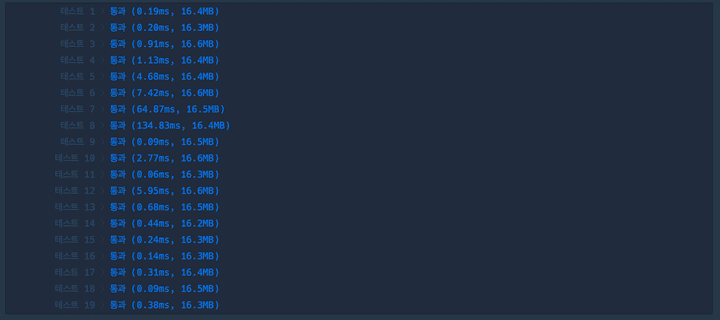
보다시피 테스트 8번에서 134 -> 40 이라는 엄청난 차이가 있다.

왜냐하면 Enumerated 메소드가 for 문으로 탐색하는 원소를 맵핑 하여 i 를 생성하기 때문에 O(N) 의 시간을 가진다고 한다..

Enumerated 알고리즘 풀때 지양하자.

이걸 어떻게 알게 됐냐면, 다른사람 코드를 테스트 해보면서 실행속도를 봤는데 나와 차이가 많이 나서 뭔가 싶어서 봤더니 Enumerated 차이가 있었던 것을 발견했다.

운좋게 이 사실을 알게되었다!

1. 문제
2. 핵심 아이디어
3. 코드
4. 풀이 과정